Problem: Bin Packing

A look into a popular problem in computer science

Introduction

The bin packing problem, a staple in computer science, exemplifies a classic challenge in algorithm design due to its intrinsic complexity. It stands out as an early computer science problem that was intractable, demanding innovative approaches for effective solutions. This article delves into several classic approximate bin-packing algorithms, presenting their implementations in Go along with practical examples.

Understanding the Bin Packing Problem

At its core, the problem is to find the minimum number of identical bins, each with a capacity C, that accommodates a finite set of weights (w_1, w_2, w_3, .., w_n). Another constraint is to ensure that no bin with its collective weights, exceeds the capacity C. Traditionally, C is set to 1 and weights are real numbers, for this discussion, we'll consider C as a positive integer and the weights as positive integers that are less than 'C'.

A crucial aspect of bin packing is the order of packing:

1. if it's fixed order (e.g, in a real-world application, the order in which they arrive) or

2. if rearrangement is possible after arrival, to optimize packing.

Algorithms designed for the former scenario are termed online algorithms, while those allowing rearrangement are known as offline algorithms. Offline algorithms, it's important to note, require additional storage for the rearrangement process.

Online and Offline Algorithms for Bin Packing

We will explore both online and offline algorithms, each presented as a function prototype in Golang.

For illustrative purposes, consider bins with a capacity of 7 and items weighing 1, 4, 9, 4, 1, 5, 8, 3, 2, 5, 7, 3, 2, and 6.

func fit(binsize uint, sizes []uint, numItems uint) uint {
    // Implementation goes here
}

The key parameters include

• binsize (the capacity 'C'),

• sizes (the array of item weights),

• bins (an array indicating the bin assigned to each item).

• numitems: The size of the sizes and bins arrays.

The function returns the total number of bins utilized.

For example, C, the capacity of the bins, is 7, and we want to pack items with the following weights: 1, 4, 9, 4, 1, 5, 8, 3, 2, 5, 7, 3, 2, 6.

func main() {
	sizes := []uint{1, 4, 9, 4, 1, 5, 8, 3, 2, 5, 7, 3, 2, 6}
	numItems := uint(len(sizes))
	bins := make([]uint, numItems)
	binsize := uint(10)

      // fit function has been defined with the above signature:
	binsUsed := fit(binsize, sizes, bins, numItems)

	fmt.Printf("%d bins were used\n", binsUsed)
	for item := range sizes {
		fmt.Printf("Item #%d (size %d) is in bin %d\n", item, sizes[item], bins[item])
	}
}

I. Next Fit Algorithm

The first algorithm we examine is the Next Fit (NF). It's straightforwardly effective:

1. Continuously place items into a bin until an item exceeds the bin's capacity.

2. Once this occurs, seal the current bin and start filling a new one.

This method is similar to real-world scenarios where bins are dispatched as soon as they are filled. It's efficient in terms of space utilization, as it keeps only one bin open at a time.

An interesting property of the algorithm is that it never uses more than twice the optimal number of bins (denoted as 'B'). This is because the combined weight of any two adjacent bins cannot exceed the bin capacity; otherwise, the second bin's contents would have fitted in the first. Hence, the combined weight of all the bins can’t be less than the total weight, so no more than 2 x B bins are required.

Here's a simplified Golang snippet to demonstrate the Next Fit algorithm:

package main

func nextFit(binsize uint, sizes []uint, numItems uint) []uint {
    bins := make([]uint, numItems)
    var bin uint = 0
    capacity := binsize

    for item := uint(0); item < numItems; item++ {
        if sizes[item] > capacity {
            // Start a new bin
            bin++
            capacity = binsize
        }
        // Put item in bin
        capacity -= sizes[item]
        bins[item] = bin
    }

    return bins
}

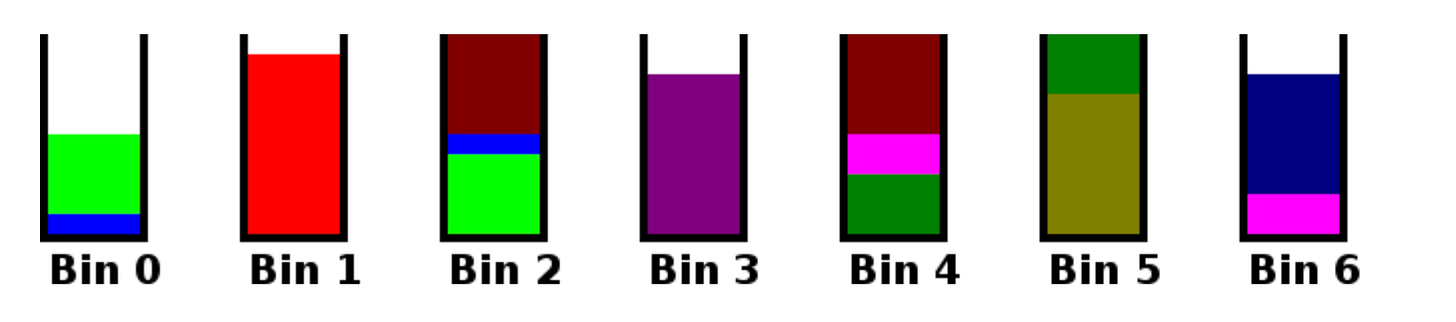
Results of the Next Fit Algorithm:

7 bins were used
Item #0 (size 1) is in bin 0
Item #1 (size 4) is in bin 0
Item #2 (size 9) is in bin 1
Item #3 (size 4) is in bin 2
Item #4 (size 1) is in bin 2
Item #5 (size 5) is in bin 2
Item #6 (size 8) is in bin 3
Item #7 (size 3) is in bin 4
Item #8 (size 2) is in bin 4
Item #9 (size 5) is in bin 4
Item #10 (size 7) is in bin 5
Item #11 (size 3) is in bin 5
Item #12 (size 2) is in bin 6
Item #13 (size 6) is in bin 6

Figure: Bin packing algorithm by next fit (NF) algorithm

II. First Fit Algorithm

Looking at the Next Fit algorithm’s results, we can see a more efficient bin utilization. Consider a scenario where we maintain an open bin, even if it cannot accommodate the next item, with the anticipation that a future, smaller item might fit. This scenario forms the crux of the First Fit (FF) algorithm, a form of greedy approximation:

1. Place each item into the first available bin that has sufficient space.

2. If no bin is found, initiate a new bin.

• Performance:

• Implementation:

  Incorporating a balanced binary search tree, such as an AVL tree, allows for an efficient O(n log n) implementation.

Consider this AVL tree-based approach for finding the first suitable bin:

// Finds the first bin in the AVL tree that can fit the data
func avlTreeFirstFit(tree *avltree.Tree, data interface{}) interface{} {
    var found interface{}
    node := tree.Root()
    for found == nil && node != nil {
        rv := tree.Compare(node.Data(), data)
        if rv >= 0 {
            found = node.Data()
        } else {
            node = node.Right()
        }
    }
    return found
}

• Remarkably, First Fit guarantees usage of no more than 2 x B, the optimal number of bins. This is because all bins can't be less than half-full; otherwise, the contents of two such bins could be merged. Research has even shown that First Fit typically uses no more than 1.7B bins.

Then we can use that to find the bin to use in the First Fit algorithm:

// finds the first bin that can accommodate the given size
func findFirstBin(tree *avltree.Tree, size uint) *Bin {
    b := Bin{ID: 0, Size: size}
    return avlTreeFirstFit(tree, &b).(*Bin)
}

// Implements the First Fit bin packing algorithm
func firstFit(binsize uint, sizes []uint, numItems uint) uint {
    binsUsed := uint(0)
    bins := make([]uint, numItems)

    tree := avltree.New(binCompare)
    if tree == nil {
        return 0
    }

    for item := uint(0); item < numItems; item++ {
        b := findFirstBin(tree, sizes[item])
        if b != nil {
            // Add to this bin
            tree.Remove(b)
            bins[item] = b.ID
            binUse(b, sizes[item])
            tree.Add(b)
        } else {
            // Create a new bin and add to it
            b = binCreate(binsUsed, binsize)
            bins[item] = binsUsed
            binUse(b, sizes[item])
            tree.Add(b)
            binsUsed++
        }
    }

    tree.ForEach(binDelete)
    tree.Delete()
    return binsUsed
}

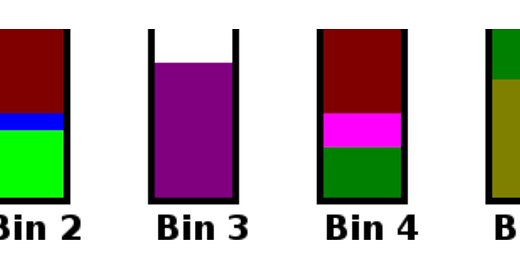
These are the results with First Fit. Notice how the bins are no longer being filled in sequence. It might use 7 bins, with items strategically placed to maximize space utilization.

7 bins were used
Item #0 (size 1) is in bin 0
Item #1 (size 4) is in bin 0
Item #2 (size 9) is in bin 1
Item #3 (size 4) is in bin 0
Item #4 (size 1) is in bin 0
Item #5 (size 5) is in bin 2
Item #6 (size 8) is in bin 3
Item #7 (size 3) is in bin 2
Item #8 (size 2) is in bin 2
Item #9 (size 5) is in bin 4
Item #10 (size 7) is in bin 5
Item #11 (size 3) is in bin 4
Item #12 (size 2) is in bin 3
Item #13 (size 6) is in bin 6

II. Best Fit (BF) Algorithm

The Best Fit (BF) algorithm takes a slightly different approach:

1. Instead of just looking for the first suitable bin, Best Fit tries to place each item in the bin that will be the fullest after the item is added. i.e., it targets the least empty bin.

2. if no bin is found, create a new bin.

Like First Fit, Best Fit also has the 1.7 × B upper bound on the number of bins used. Also similar to First Fit, Best Fit can be implemented in O(n log n) time using an AVL tree.

// finds the best bin in the AVL tree that can fit the data.
func avlTreeBestFit(tree *avltree.Tree, data interface{}) interface{} {

    var best interface{}
    var found bool
    node := tree.Root()

    for node != nil && !found {
        result := tree.Compare(node.Data(), data)
        if result > 0 {
            if best == nil || tree.Compare(node.Data(), best) < 0 {
                best = node.Data()
            }
            node = node.Left()
        } else if result < 0 {
            node = node.Right()
        } else {
            best = node.Data()
            found = true
        }
    }

    return best
}

We can now use this to find the bin to use in the Best Fit algorithm:

// finds the best bin that can accommodate the given size.
func findBestBin(tree *avltree.Tree, size uint) *Bin {
    b := Bin{ID: 0, Size: size}
    return avlTreeBestFit(tree, &b).(*Bin)
}

// implements the Best Fit bin packing algorithm.
func bestFit(binsize uint, sizes []uint, numItems uint) uint {
    binsUsed := uint(0)
    bins := make([]uint, numItems)

    tree := avltree.New(binCompare)
    if tree == nil {
        return 0
    }

    for item := uint(0); item < numItems; item++ {
        b := findBestBin(tree, sizes[item])
        if b != nil {
            // Add to this bin
            tree.Remove(b)
            bins[item] = b.ID
            binUse(b, sizes[item])
            tree.Add(b)
        } else {
            // Create a new bin and add to it
            b = binCreate(binsUsed, binsize)
            bins[item] = b.ID
            binUse(b, sizes[item])
            tree.Add(b)
            binsUsed++
        }
    }

    tree.ForEach(binDelete)
    tree.Delete()
    return binsUsed
}

Comparing them to First Fit, notice how item #11 was placed in bin 5, rather than bin 4 because bin 5 had the lesser amount of free space while still being able to accommodate it.

With the same set of items, Best Fit might also use 7 bins, but the distribution of items across the bins will likely be more compact.

7 bins were used
Item #0 (size 1) is in bin 0
Item #1 (size 4) is in bin 0
Item #2 (size 9) is in bin 1
Item #3 (size 4) is in bin 0
Item #4 (size 1) is in bin 0
Item #5 (size 5) is in bin 2
Item #6 (size 8) is in bin 3
Item #7 (size 3) is in bin 2
Item #8 (size 2) is in bin 2
Item #9 (size 5) is in bin 4
Item #10 (size 7) is in bin 5
Item #11 (size 3) is in bin 5
Item #12 (size 2) is in bin 3
Item #13 (size 6) is in bin 6

Figure: Visual representation of bin packing following the Best Fit approach.

Comparative Results: When comparing Best Fit to First Fit, subtle differences in bin utilization become apparent. For instance, an item might be placed in a different bin than it would have been under First Fit, due to Best Fit's strategy of filling the bins as tightly as possible.

III. Worst Fit (WF) Algorithm

Exploring further into the bin packing algorithm spectrum, we encounter the Worst Fit (WF) method, which can be seen as the antithesis of the Best Fit approach. Where Best Fit seeks the tightest fit, Worst Fit aims for the opposite:

• Strategy: The goal is to place each item into the bin with the most available space, effectively using the least full bin that can still accommodate the item.

• Implementation Consideration: Interestingly, the optimal data structure for implementing Worst Fit is a heap, specifically a max heap. This choice stems from the need to consistently identify the bin with the most space available efficiently.

Here's a peek into a Worst Fit implementation using a max heap in Go:

func worstFit(binsize uint, sizes []uint, numItems uint) uint {
    binsUsed := uint(0)
    bins := make([]uint, numItems)
    heap := &BinHeap{}

    heap.Init()

    for item := uint(0); item < numItems; item++ {
        var b *Bin
        if heap.Len() > 0 {
            b = heap.Pop().(*Bin)
            if b.Capacity < sizes[item] {
                // Too small; put b back
                heap.Push(b)
                b = nil
            }
        }
        if b == nil {
            // Create a new bin
            b = binCreate(binsUsed, binsize)
            binsUsed++
        }
        bins[item] = b.ID
        binUse(b, sizes[item])
        heap.Push(b)
    }

    // Assuming binDelete is a function that handles bin deletion
    for heap.Len() > 0 {
        binDelete(heap.Pop().(*Bin))
    }

    return binsUsed
}

Performance Insight: When analyzed against Best Fit, the Worst Fit strategy leads to a different allocation pattern, as it consistently seeks to use the least full bins.

Example: In a specific scenario, Worst Fit may use 7 bins, but the placement of items like item #12 in a less filled bin (bin 5 instead of bin 3) illustrates its distinct strategy.

7 bins were used
Item #0 (size 1) is in bin 0
Item #1 (size 4) is in bin 0
Item #2 (size 9) is in bin 1
Item #3 (size 4) is in bin 0
Item #4 (size 1) is in bin 0
Item #5 (size 5) is in bin 2
Item #6 (size 8) is in bin 3
Item #7 (size 3) is in bin 2
Item #8 (size 2) is in bin 2
Item #9 (size 5) is in bin 4
Item #10 (size 7) is in bin 5
Item #11 (size 3) is in bin 4
Item #12 (size 2) is in bin 5
Item #13 (size 6) is in bin 6

Figure: Bin packing by Worst Fit (WF) algorithm

IV. First Fit Decreasing (FFD) Algorithm

The order in which items are introduced to the bin packing algorithms significantly influences their efficiency. This observation lays the groundwork for the First Fit Decreasing (FFD) algorithm:

1. Sort the items to be inserted in decreasing order by size

2. Go through the items in sorted order

   1. Try to place the item in the first bin that will accommodate it

   2. If no bin is found, start a new bin

The FFD algorithm is particularly effective, with a proven upper bound of using at most (4B + 1) / 3 bins if the optimal number is B

To implement FFD, we need utilities for comparison and sorting of unsigned integers in decreasing order:

// A helper function to compare two uints in decreasing order.
func compareUintDecreasing(a, b uint) int {
    if a > b {
        return -1
    }
    if a < b {
        return 1
    }
    return 0
}

// sorts an array of unsigned integers in decreasing order.
func sortUintsDecreasing(sizes []uint) {
    sort.Slice(sizes, func(i, j int) bool {
        return compareUintDecreasing(sizes[i], sizes[j]) < 0
    })
}

func main() {
    // Example usage
    sizes := []uint{3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5}
    sortUintsDecreasing(sizes)
    // sizes is now sorted in decreasing order
}

With these utilities, we can sort the items and apply the First Fit algorithm:

// Performs the First Fit Decreasing algorithm for bin packing.
func firstFitDecreasing(binsize uint, sizes []uint, numItems uint) uint {
    sortUintsDecreasing(sizes)
    return firstFit(binsize, sizes, numItems)
}

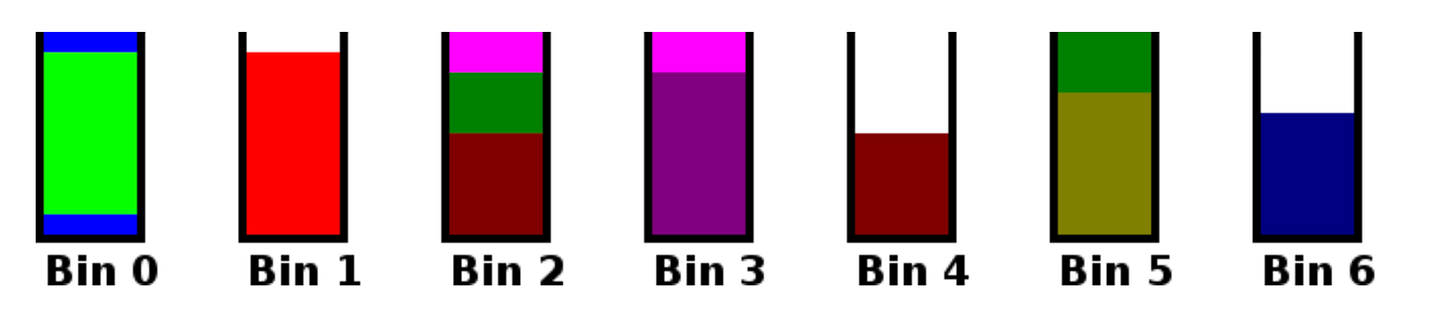
These are the results. Notice that this time we have an optimal packing, with only 6 bins used. I got an optimal packing like this for all of the offline algorithms.

6 bins were used
Item #0 (size 9) is in bin 0
Item #1 (size 8) is in bin 1
Item #2 (size 7) is in bin 2
Item #3 (size 6) is in bin 3
Item #4 (size 5) is in bin 4
Item #5 (size 5) is in bin 4
Item #6 (size 4) is in bin 3
Item #7 (size 4) is in bin 5
Item #8 (size 3) is in bin 2
Item #9 (size 3) is in bin 5
Item #10 (size 2) is in bin 1
Item #11 (size 2) is in bin 5
Item #12 (size 1) is in bin 0
Item #13 (size 1) is in bin 5

Figure: Bin packing by First Fit Decreasing (FFD) algorithm

V. Best Fit Decreasing (BFD)

The Best Fit Decreasing (BFD) algorithm builds on the principles of the Best Fit strategy with a crucial preprocessing step:

1. Sort the items to be inserted in decreasing order by size

2. Go through the items in sorted order

   1. Try to place the item in the fullest bin that will accommodate it, i.e., the one that will leave the least space remaining

   2. If no bin is found, start a new bin

// Performs the Best Fit Decreasing algorithm for bin packing.
func bestFitDecreasing(binsize uint, sizes []uint, numItems uint) uint {
    sortUintsDecreasing(sizes)
    return bestFit(binsize, sizes, numItems)
}

Insights: Interestingly, BFD often mirrors the results of the First Fit Decreasing (FFD) algorithm, suggesting a similar level of efficiency in optimal packing conditions.

VI. Worst Fit Decreasing (WFD)

Parallel to BFD, the Worst Fit Decreasing (WFD) algorithm is an adaptation of the Worst Fit strategy:

1. Sort the items to be inserted in decreasing order by size

2. Go through the items in sorted order

   1. Try to place the item in the least full bin that will accommodate it, i.e., the one that will leave the most space remaining

   2. If no bin is found, start a new bin

Here's how WFD might be implemented:

// Performs the Worst Fit Decreasing algorithm for bin packing.
func worstFitDecreasing(binsize uint, sizes []uint, numItems uint) uint {
    sortUintsDecreasing(sizes)
    return worstFit(binsize, sizes, numItems)
}

Insights:

Though WFD often yields results similar to other offline algorithms, subtle differences in packing order can be observed. For example, the placement of specific items like #10 and #11 may vary depending on the available space at the time of packing. However, the overall efficiency remains consistent due to the items' sizes.

6 bins were used
Item #0 (size 9) is in bin 0
Item #1 (size 8) is in bin 1
Item #2 (size 7) is in bin 2
Item #3 (size 6) is in bin 3
Item #4 (size 5) is in bin 4
Item #5 (size 5) is in bin 4
Item #6 (size 4) is in bin 3
Item #7 (size 4) is in bin 5
Item #8 (size 3) is in bin 5
Item #9 (size 3) is in bin 2
Item #10 (size 2) is in bin 5
Item #11 (size 2) is in bin 1
Item #12 (size 1) is in bin 0
Item #13 (size 1) is in bin 5

Item Packing Example: Using WFD, a typical result might be the use of 6 bins, with items strategically placed based on the available space at the time of their insertion.

Conclusion: The Spectrum of Bin-Packing Algorithms

This exploration into approximate bin-packing algorithms reveals their often optimal performance, especially in offline scenarios. Yet, the quest for optimal solutions continues to drive research. A notable mention is the Bin Completion technique (Korf, 2002), considered one of the fastest known optimal algorithms to date.

The bin-packing problem, with its various algorithms and continuous research, exemplifies the dynamic nature of computer science and optimization problems. Whether through heuristic approaches like BFD and WFD or more exact methods like Bin Completion, the challenge of efficiently packing bins continues to intrigue and inspire researchers and practitioners alike.